Run or Train Transformer Models On Your Consumer GPU With Quantization
State Of The Art Models Shouldn't Be Inaccessible
👋 Hi, this is Ruite. My newsletter is here to make you feel good and help you get better at Python and machine learning.
If interested in any of those subjects, consider subscribing to the newsletter 😊.
Thank you for your patience.
It took me a lot of time to finish this post, 4 weeks or more now.It is not that this piece is the most definitive piece on quantization, hahaha; I just prioritized other life stuff.
This post was inspired by a course called Quantization Fundamentals from Deeplearning AI and Hugging Face. Do check it out.
I wanted to write this piece because everybody should be able to use and access large language models. Their capabilities are exciting and wide-ranging, and they are fun to play with!
The top applications that come to my mind are:
You can train your AI chatbot or assistant for more privacy when translating, summarizing, text-to-image, and text generation.
You can have a free code assistant for the same reasons.
If you are a life science researcher like myself, LLMs are revolutionizing the field, from drug discovery and protein generation to 3D structure prediction. Think of ESMFold.
The possibilities are just endless!
But the models have been getting bigger and bigger. There is now a huge gap between the size of open source SOTA models, around 70B parameters or 280 GB, and the largest GPU hardware, 100 GBs on the commercial side and 24 GBs for consumer GPUs.
As you can see, running these models can be challenging and, in most cases, expensive and out of reach by most of the open-source community.
So, we need ways to make these models more accessible for inference and fine-tuning to downstream tasks.
The different data types and how they affect model size
Neural networks have parameters called weights and biases, which are matrices with numbers.
These numbers
Share a data type: floats or integers.
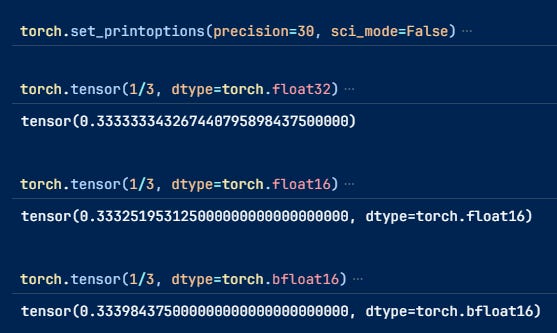
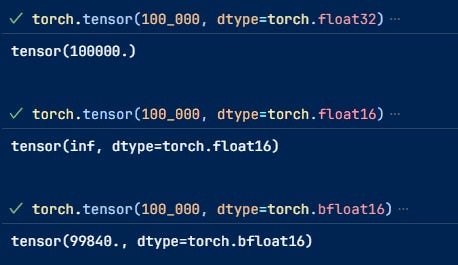
Have a specific range and precision determined by the bits it uses. The more bits, the more range of numbers and decimals it can handle before turning into inf or 0 (overflow and underflow). You can view the different data types Pytorch supports here.
Consume memory; for each 8 bits, 1 byte.
For example, the standard way of storing model weights, the float32 format (floating point with 32 bits), consumes 4 bytes of memory per parameter. So, a 70B parameter model occupies 280 GB of memory.
However, you can represent the data in other data types by reducing the number of bits like float16, bfloat16, int8, float4, etc, which obviously reduces the range of numbers you can represent and their precision.
Here is an intuitive example to show the differences. I took it from a newsletter by Sebastian Raschka, PhD. But I cannot find it; I will put it here if somebody can send it to me.
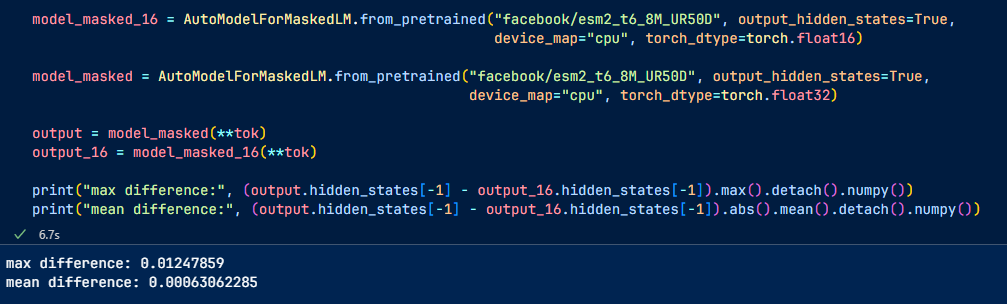
Most models can be used with float16 or bfloat16, halving memory requirements without losing performance. Because the numbers they can represent are still sufficiently large.
However, when we go down to lower bits like int8 or less, things start to get trickier because they cannot represent the same range of numbers, which means you need a way to map these values, a process called quantization.
One example is linear quantization.
We first map the original vector's min and max values to the new datatype's min and max values. For int8 would be [-128, 127]
Then, apply this formula to map the rest of the values:
\(q = \frac{r}{s} + z \)q is the value in the new datatype, and r is the original value. s and z are quantization factors
S and Z can be calculated as follows:
\(r_{\text{min}} = s \left( q_{\text{min}} - z \right)\)\(r_{\text{max}} = s \left( q_{\text{max}} - z \right) \)we subtract
\(s = \frac{r_{\text{max}} - r_{\text{min}}}{q_{\text{max}} - q_{\text{min}}} \)\(z = int \left( \text{round} \left( q_{\text{min}} - \frac{r_{\text{min}}}{s} \right) \right) \)De-quantize by applying the 2nd formula again.
This process causes small rounding errors since we are quantizing integers, but there are ways to reduce these errors. In addition, the quantization and de-quantization process will increase the inference latency.
There is a trade-off between memory and speed.
Let's look at different methods for inference and fine-tuning at these lower bits while preserving the prediction quality as much as possible.
Inference
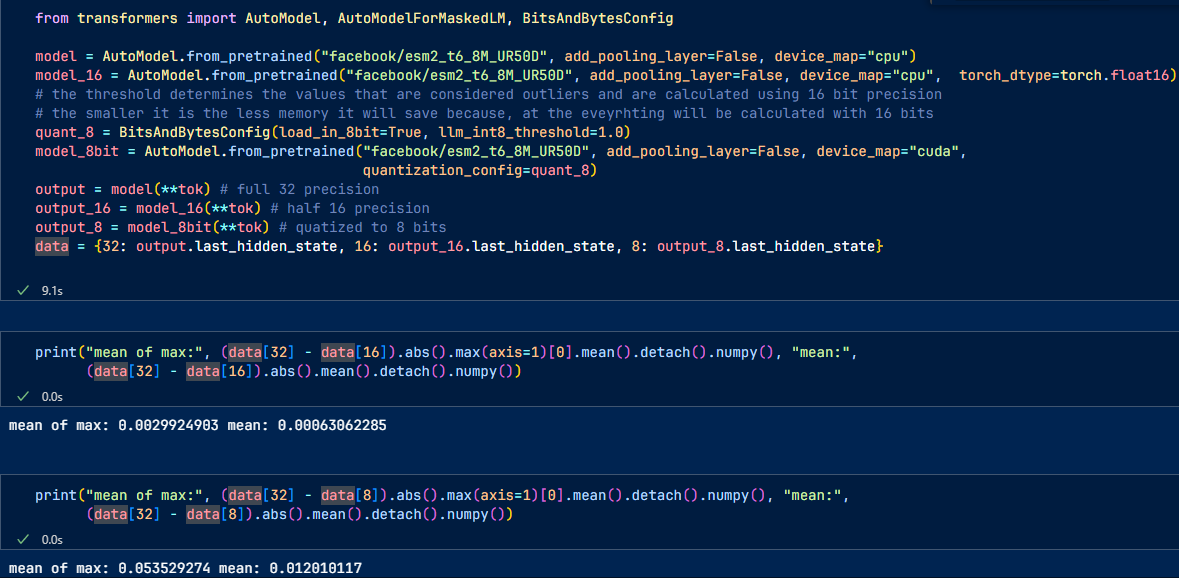
Int8 inference with bitsandbytes from Hugging Face
The linear mapping suffers one problem. It is susceptible to outliers.
Research from Tim Dettmers and Hugging Face discovered that the LLMs’ hidden layers contained outliers, which increase in frequency and magnitude with the increasing size of the model.
Luckily, these outliers happen only in particular columns of the hidden states.
So what they do is just:
Extract the outliers from the hidden states (values that are larger than a certain threshold).
Perform the matrix multiplication of the outliers in FP16 and the non-outliers in int8.
Dequantize the non-outlier results and add outlier and non-outlier results to receive the full result in FP16.
You can learn more from this post.
It is very easy to do with Hugging Face and bistandbtes
Still, there will be some rounding errors.
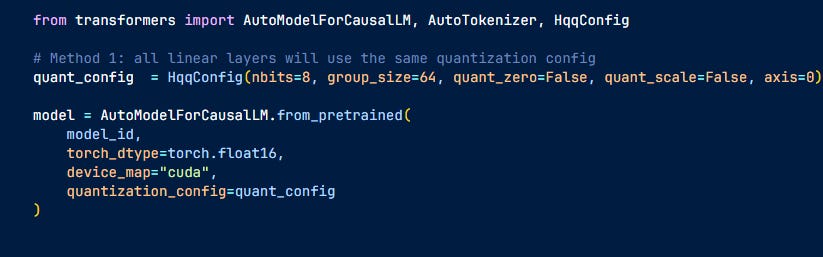
HQQ or Half-Quadratic Quantization
What if we need lower bits like 4, 3, 2, or even 1 bit? The performance would degrade too much and might require some calibration data to minimize the errors between the original layer output and the quantized output.
However, as you might intuitively know, this is costly because you need to get the data and do some training.
Here is where HQQ comes in. It doesn't use calibration data, so it is fast but still achieves results that are competitive with the calibration methods.
Instead of minimizing the output errors, they try to find the quantization parameters (zero-point z and scaling s) that minimize the difference between the original weights and their de-quantized version, eliminating the need for data.
It easily integrates with Hugging Face models. That's it, the model has been quantized
Fine-tuning with QLoRa
Fine-tuning is oftentimes necessary to adapt the models to your task.
Still, training in full precision would be quite memory-intensive since you have to consider not only the model size but also the optimizers, gradients, etc. Adam optimizers, for example, store 2 additional parameters for each trainable parameter.
This is where QLoRA comes in. QLoRA is an extension of LoRA to reduce LLMs’ memory footprint even more without losing performance.
LoRa trains a small number of matrices A and B with rank m X r and r X n, the product of which has the same rank as the weight matrices in the LLMs, m X n. However, since r is usually a small number between 8 and 256; the total number of trainable parameters is just a small % of the original parameters that are frozen during training.
Then, these LoRA matrices are added to the weights of the attention layers to create the fine-tuned model.
You can find an in-depth explanation of LoRa here if you want to know more
QLoRa adds 3 features to LoRa:
4-bit NormalFloat quantization of the weights during training. For forward and backward passes, the weights must be de-quantized to 16 bits so the training will be slower.
Double quantization of the quantization factors. To reduce the effect of outliers, the quantization is done in groups, which means you'll need to store quantization factors like s and Z for each group. As the number of parameters increases, memory consumption of these factors can become significant.
Paging with unified memory: it unifies the memory of CPUs and GPUs to ensure data transfer is easier and error-free. If GPUs run out of memory, for example, it can send the task to the CPU's memory
Here is a nice tutorial on how to fine-tune with QLoRa using Hugging Face
Towards 1-bit LLMs with HQQ
4 bits is not the lowest you can go when fine-tuning models with LoRA; the HQQ group showed that you could quantize the models to 2-bit and 1-bit,
See this blog post, where they fine-tuned a 2-bit Llama 2 -7B, achieving better results in some benchmarks than the full precision Llama 2-7B and some smaller models.
If you enjoyed reading this post or found it useful, consider commenting.
I always want to hear your thoughts! Or consider clicking the ❤️ button on this post so more people can discover it.
See you next time!